As the COVID-19 pandemic continues to take thousands of lives every day in different parts of the world, vaccine and antiviral research is continuing, as the only hope of emergence from under the shadow of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). However, a recent study by researcher Bhavin S Khatri at Imperial College London and published on the preprint server medRxiv* in August 2020 suggests that the SARS-CoV-2 virus may die out more rapidly than thought, provided the reproduction number is kept low.
The SIR Model
The SIR (Susceptible-Infected-Recovered) model has remained one of the best-used models to understand the evolution of an epidemic since it was first introduced. SIR simplifies many factors related to disease transmission across different populations and locales and periods of time. However, its strength lies in its ability to condense the epidemic into a few key parameters.
One of the most critical factors that determine the course of an epidemic is the effective reproduction number or Re (not to be confused with the R0, basic reproduction number), which shows growth at a value above 1, and shrinkage when below 1. It also conveys the number of infections occurring as a result of spread from primary cases as 1/γ. Simple parameters can represent the broad outlines of more detailed models, offering a better idea of how changes in these parameters affect the epidemics, though at the cost of the quantitative accuracy offered by more tightly parameterized models. A combinatorial approach could thus help predict epidemic behavior more accurately.
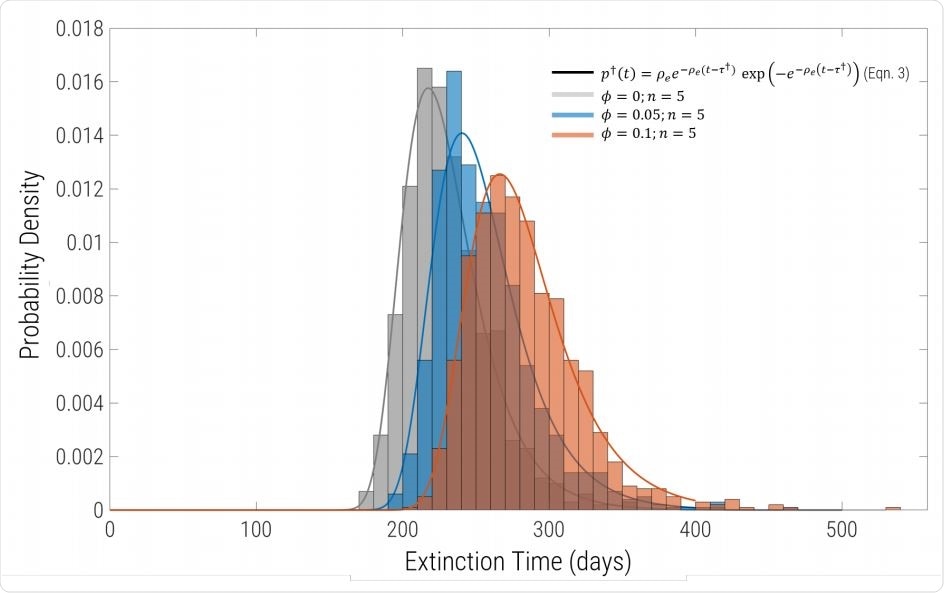
Probability density of extinction times for the same parameters as in Fig.1, but including migration and sub-division into equal sized populations. Each histogram comprises 1000 replicates for n = 5 regions connected by uniform migration with probability φ. Grey bars are φ = 0 (complete isolation), blue correspond to φ = 0.05 and φ = 0.1 are the red bars. For φ = 0 the solid line grey line is exactly the solid black line in Fig.2, showing that the extinction time distribution of identical to the single global well-mixed population of same aggregate size. The solid blue and red lines are fits to the histogram using Eqn.7 with a single free parameter Re (with γ and I0 constrained to the values used to run the simulations.
*Important notice: medRxiv publishes preliminary scientific reports that are not peer-reviewed and, therefore, should not be regarded as conclusive, guide clinical practice/health-related behavior, or treated as established information.
Individual Discreteness
The current study deals with the SIR model while incorporating individual discreteness. This makes it different from deterministic models where the number and density of infected individuals are treated as continuous so that the value of the density can actually become less than 1. This can lead to the wrong prediction of a second wave after restrictions on movement are lifted. Instead, this model uses a full stochastic description at low densities, while tracing the course of the outbreak. Under such conditions, the number of individuals in a population can be exactly 0, which means the epidemic is extinct when the infection number is 0. Unless cases are imported, no second wave can occur.
The paper considers the current situation where herd immunity has not yet been reached, but the Re is less than one. The epidemic is, therefore, not growing, but there are many susceptibles for each infected person. The researchers found that by using a new threshold I† = 1=(1 - Re), representing the extinction time, it could be shown that as Re is between 0.6 and 1, the mean extinction time drops significantly compared to a deterministic model.
Extinction Time Depends on Re
To capture the effects of geographical variations and other differences, Khatri compared it to more complex as well as simpler models. He found that by simply rescaling Re to include the effect of migration, they could arrive at an accurate distribution of extinction time.
Using this theory, Khatri predicted that with Re between 0.6 and 1, extinction times would cover many years. In this interval, the deterministic model consistently overshoots the mark significantly. However, if it is kept below 0.5, it can drop to months, within a single year. As the Re drops further below this, there is not much benefit in terms of reducing the extinction times further.
Finally, as the mean infection duration 1/γ increases, extinction time increases as well. Recent research shows that asymptomatic infection duration is 7 days on median, while the presymptomatic and symptomatic infection duration is 2 days on average, and 13.4 days median. The mean duration of infection is 20 days or so, according to the early studies. Among these, the duration of asymptomatic infection is probably the most important since it is during this period that infection is most likely to be carried to others.
Extinction Time in the UK and Globally
The current model, therefore, assumes that the duration of infection in terms of infectious potential is 7 days on average. Then the model concerning the UK shows that the epidemic can die out in about 100 days, provided the Re is below 0.5. The UK government’s estimate, however, as well as that of the MRC Biostatistics Unit, Cambridge, puts the Re at the end of June as 0.9 for England. At this value, extinction would take almost two years.
For the world’s population of 7.8 billion, and an incidence of 0.05%, the predicted extinction time is approximately the same for Re below 0.5, at 200 days (6-7 months). But with an Re above 0.6, it will take many years to die out. In more detailed terms, they predict that if the Re is 0.4 and if the infection duration is 7 days, the extinction time would be about 177 days.
The simple model was evaluated by simulating the conditions using a realistic spatial epidemic simulator, GleamViz. The investigator found that extinction times predicted by both methods match reasonably well. Khatri says, “Despite the heterogeneity of contacts between different regions, the overall decay of infection is exponential, and the stochastic variation follows closely the well-mixed predictions of the stochastic SIR model presented here.”
Implications and Conclusion
The predictions at global level should be considered as an approximate guide if all countries follow the same kind of action plan. The researchers also caution that if a nonhuman reservoir exists, harboring the virus, this could enable the virus to reinfect human populations. In this special scenario, extinction would be only a temporary state. This can be accounted for in a similar way to human importations, but if such reservoirs can be identified and surveyed, this route can also be sealed.
Describing his theory as one which provides “a useful and quick guide to estimate the time to extinction of an epidemic,” Khatri concludes, “The broad conclusion when applied to SARS-Cov-2 is that to achieve rapid extinction, on times of order or less than half a year, then the goal should be to restrict Re to numbers much less than 1 and optimally in the region Re ≈ 0:4 → 0:5.’
*Important notice: medRxiv publishes preliminary scientific reports that are not peer-reviewed and, therefore, should not be regarded as conclusive, guide clinical practice/health-related behavior, or treated as established information.
BMI's influence on disease pathogenesis uncovered in new research