Quantum computing to predict RNA secondary structures

By Sam HancockReviewed by Benedette Cuffari, M.Sc.Apr 13 2022

The use of computational methods to investigate the complex secondary structures of ribonucleic acid (RNA) molecules has long been of significant importance for biological research and drug development, especially with the rise of synthetic RNAs.

Study: RNA folding using quantum computers. Image Credit: Gorodenkoff / Shutterstock.com

The secondary structures of RNA molecules can impact their stability, their function in translation and transcription, as well as their compactness. However, verifying secondary structures through experimental methods is extremely time-consuming.

Although computational methods can vary significantly, many are limited in their ability to deal with structures including pseudoknots. In fact, even the most efficient methods to solve RNA secondary structures cannot effectively solve pseudoknots.

In a recent PLOS Computational Biology study, researchers investigate the possibility of using quantum computing to create methods that can more effectively and rapidly solve these structures.

Background

Quantum computers are often categorized as either gate models or quantum annealing. Quantum annealers, for example, have a much more narrow range of applications than gate modeling systems and focus on optimizing solutions to problems by minimizing a problem Hamiltonian.

The prediction for the RNA secondary structure was implemented as a binary quadratic model (BQM)on a D-wave quantum annealer (QA) with a Hamiltonian designed to optimize the number of non-overlapping consecutive base pairs. Pseudoknots imposed penalties and additional constraints were used to prevent bases from forming more than one pair.

Classical data was encoded onto a quantum device, with each possible stem mapped to a single qubit. The qubits that return a value of one upon measurement represent stems that contribute to a secondary structure.

The equation uses an energetic term rewarding longer stems and two tunable constants. The final secondary structure can then be determined by recording the values of all qubits and saving any stems that were represented by qubits returning ‘1’.

However, if the Quantum Processing Unit (QPU) is directly loaded with the BQM, the data returned is significantly noisy, with a greater number of qubits exacerbating the issue. The D-wave uses a classical device as a hybrid solver, which breaks down the problem into smaller elements before handing them to the QPU to solve.

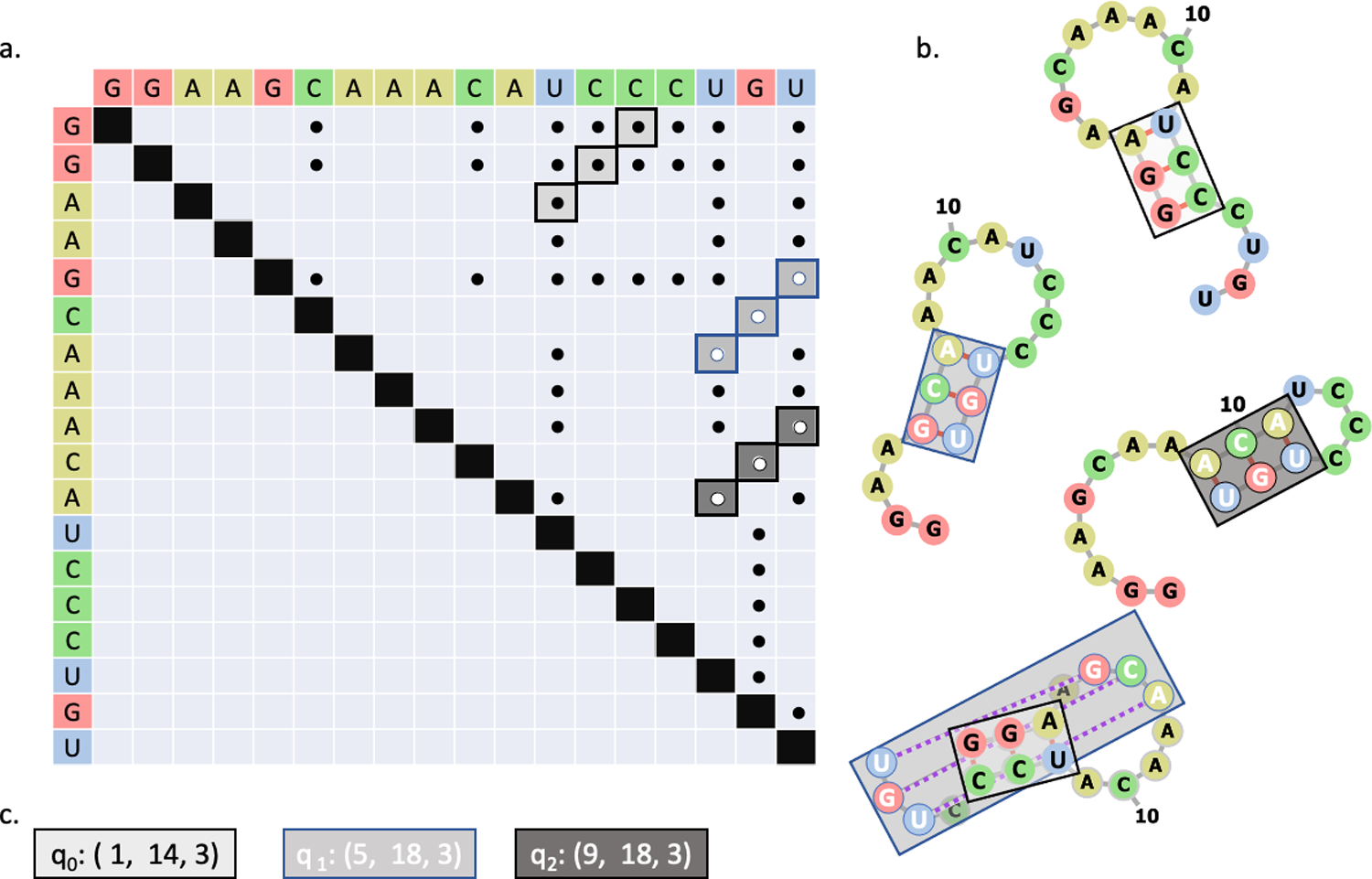(a) Matrix representation of potential base pairs. Stems are highlighted in shades of gray and outlined in black or blue. The colors serve only to help distinguish the stems. (b) Structural representations of stems. Grey lines indicate covalent bonds, red lines indicate base pairing, and dashed purple lines represent base pairs in a pseudoknot configuration. The color of the boxes map to the stems identified in (a). (c) Each possible stem is assigned to a qubit on the quantum device. If the qubit returns “1”, then the associated stem is included in the RNA secondary structure. Otherwise, the stem is excluded. 

Study findings

In the current study, an MPI-enabled solver was written to compare against the hybrid solver. Using this method, systems containing 45 qubits can be solved in less than 24 hours using 7,900 central processing unit (CPU) cores.

The structure predicted by the algorithm is then compared to the known solution, with sensitivity reflecting the fraction of base pairs correctly identified and specificity reflecting the fraction of base pairs mapped to the structure in the correct order.

Pseudobase was scraped for examples of RNA sequences with confirmed pseudoknots to use as a test set, with any sequences with similarities above 95% excluded.

Most sequences yielded too many possible stems for each enumeration. Thus, the length of the smallest possible stem was increased to four, excluding the shortest stems and reducing the solution space size. The final test set contained 27 sequences and a basic test showed a sensitivity of 0.97 and specificity of 0.93.

Systems containing between 45 and 881 stems were evaluated using both the quantum computing and a parallel replica-exchange Monte Carlo (REMC) algorithm method. The REMC method showed slightly higher sensitivity and specificity than the QC method; however, on average, the results were very similar.

The researchers then chose to compare these results to three existing algorithms found in current literature including SPOT-RNA, ProbKnot, and ViennaRNA. While the first two algorithms are capable of predicting pseudoknots, Vienna RNA is not.

As expected, Vienna RNA performed the worst out of all the methods, followed by ProbKnot and SPOT-RNA. Notably, SPOT-RNA performed almost as well as QC on datasets with more than 45 stems, although not as well on datasets with less.

Conclusions

The findings from the current study demonstrate that it is possible to develop a classical folding potential mapped to quantum hardware. While this approach did not outperform select current methods, it provides proof of concept for more in-depth development of similar methods in the future.

The researchers here provide many ways by which this type of system could be improved, such as by enabling the model to account for non-Watson-Crick or wobble pairs. Quantum computing, therefore, has the potential to be incredibly helpful for future attempts at solving RNA folding, as minimum energy solutions for large combinatorial search spaces can be found rapidly. Furthermore, QCs have the flexibility to employ more complex potentials, which could lead to greater specificity and sensitivity in the future.