Characterization of Worm-Like Micelles Based on Rheology

Exploring the characteristics of worm-like micelles (WLMs) has been the focus of numerous academic and industry-based studies. The applications of WLMs are spread across a broad range of industries, from oil recovery to personal care. High levels of viscosity and viscoelasticity can be easily achieved with WLMs at low costs. WLMs can also be converted into ‘smart’ or stimuli reactive structures, which can transform into a different phase that exhibits a completely different rheology. This characteristic of WLMs is useful for applications in drug delivery, biomedical and for separations based on microfluidic devices.

Worm-like micelles are formed from varied surfactant systems – cationic, anionic or zwitterionic, and from various block copolymers as well. A striking feature of WLMs is that though they are formed from different chemical groups, their rheological response is strikingly alike and they exhibit a well-defined rheological signature. All the theoretical concepts revolving around WLMs have been accepted widely and established strongly, and help in the identification of their distinct rheological signature and key structural parameters.

Based on theoretical concepts, researchers are now able to determine the effect of formulation conditions, such as the surfactant composition, pH, and the electrolyte level, on the microstructure of the WLMs. Surfactants are the most common source of WLMs. They are amphiphilic molecules and can organize themselves into various microstructures based on the surfactant packing parameter, as shown in Table 1.

Table 1. Impact of Packing Parameter on the formed surfactant microstructure

It can be seen that for a packing parameter that ranges between 1/2 and 1/3, the surfactant molecules are arranged into a rod like micellar structure. When there is an increase in concentration, these rod-like micelles grow further depending on their thermodynamics. They transform into worm-like micelles when an electrolyte or co-surfactant is added, and then finally transform into nematic liquid crystals (Figure 1).

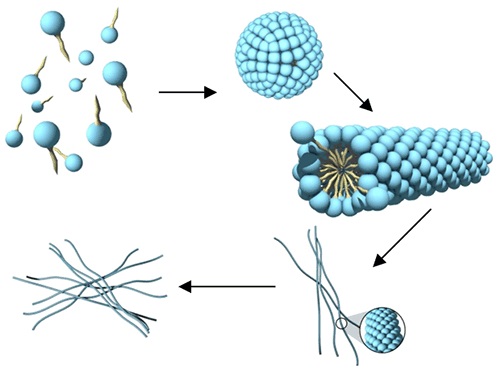
Figure 1. Phase behavior within the worm-like micelle microstructure

Unique rheological characteristics are exhibited by each of the phases illustrated in Figure 1. The most prominent and well-defined rheological signature that these phases exhibit is of a semi-dilute and concentrated worm-like micelle. Using rheology, the phase transformations from dilute to semi-dilute and the concentrated to nematic can be tracked. WLMs are the main rheology building structures in numerous applications, and therefore, industrial and academic scientists are looking to gain a thorough understanding of their rheological signature, and the effect of altering the formulation on their structure and corresponding rheology. Characteristics like micellar growth, branching, entanglement, and transitions due to shear can be studied through rheology.

Theoretical Concepts

Worm-like micelles are long and pliable like polymers, and the entanglement of the worm-like micelles is the cause of their remarkable viscosity and viscoelasticity. The two main structural characteristics that influence their rheological response are contour length (L,) which represents the end-to-end distance, and the persistence length (l_p), which represents the flexibility of the micelle.

The worm-like micelle’s hydrodynamic correlation length (x_H) influences the elasticity of the system. The relaxation of stress in a WLM happens in the same fashion as in polymers through reptation, re-forming and breaking. Reptation is the relaxation of stress through a snake-like movement of a polymer through a tube formed by its neighbors, the stress is completely relaxed when it leaves the tube.

Reptation time is determined by the volume fraction j and is calculated as: t_rep ~ L³j^3/4.

The forming or breaking time is calculated as: t_break ~ 1/L.

At the point when t_break exceeds t_rep, the micelles’ behavior is very similar to unbreakable polymers and the exponential polydispersity and stress relaxation are expressed by the following equation:

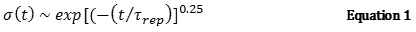
When t_break is less than t_rep and the relaxation time is given by t = (t_break t_rep)^1/2, the fluid’s behavior resembles that of a Maxwell fluid, as represented by the equations below:

The relation between the zero shear viscosity (η₀) and the plateau modulus G_p is given by the equation below:

In the above equation, the value of τ derived from the inverse of the angular frequency ω_c at the point where G' and G" intersect.

Calculation of the Hydrodynamic Correlation Length (x_H)

The value of x_H can be obtained from the plateau modulus (Equation 5). In Equation 5, k_B is the Boltzmann Constant and T is the temperature in Kelvin. The measured value of x_H is in nanometers.

Calculating the Entanglement Length (le)

Once the persistence length is estimated, or derived from high frequency rheology via Small Angle Neutron Scattering or Microrheology, the entanglement length can be calculated with Equation 6:

Experimental Procedure

This experiment evaluated a worm-like micelle structured bodywash to obtain its hydrodynamic correlation length and relaxation time. Kinexus rheometer with a cone and plate measuring system and a Peltier plate cartridge was used for rotational rheometer measurements at 25^ºC, with the help of standard pre-configured sequences in the rSpace software.

The use of a standard loading sequence ensured a loading protocol that is consistent and controlled. A strain value within the LVER was used to perform the frequency test between 0.2 and 40 rad/s. From the frequency sweep, a Cole-Cole plot (a G' and G" plot) was automatically obtained to corroborate that the WLM’s characteristic semi-circular shape (Maxwell response) was produced or not. The G_p and t values were obtained from the frequency sweep data and the x_H that was estimated from the former.

Results and Discussion

Figure 2(a) shows the frequency response of G',G'' for the bodywash product and Figure 2(b) shows the corresponding Cole-Cole plot.

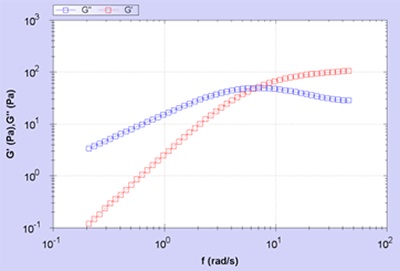
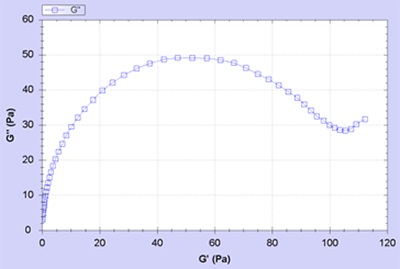
Figure 2. (a) G', G'' plotted as a function of angular frequency (b) plotted against each other (Cole-Cole plot)

Figure 2(a) shows data similar to the data expected out of a single relaxation time Maxwell model with the start of a plateau in G' at high frequencies (G_p) and an overlap in G'/G" at ω_c = 1/t. The Cole-Cole plot is in the form of a semicircle, which corroborates Maxwell behavior. A majority of transparent shampoo or bodywash products exhibit this behavior, where the combination of anionic and zwitterionic surfactants form worm-like micelle structures are formed in the presence of salt.

In case of complex formulations where additives like perfume and pearlescent agents are present, there is a deviation from a purely entangled worm-like micelle system. The occurrence of such deviations in the absence of additives can be caused by changes in the surfactant system’s microstructure and structuring efficiency. It is highly desirable to have the capability of forming a completely entangled worm-like micelle system at low salt and surfactant levels as it is considered as a highly efficient structuring system. Table 2 shows the structural parameters obtained for such a system using theoretical concepts.

Table 2. Structural parameters extracted from measurement data using theory

Conclusion

Most of the applications of WLMs are based on their underlying microstructure. By supporting theoretical concepts with rheological measurements, critical microstructural parameters, including hydrodynamic correlation time and relaxation time can be obtained. A material and its rheological behavior are characterized and described by these parameters.

Notes

Note that a parallel plate geometry or a cylindrical geometry can also be used. The use of a solvent trap is also recommended for these tests since evaporation of solvent (e.g. water) around the edges of the measuring system can invalidate the test, particularly when working at higher temperatures.

References

1. Structure & Rheology of Complex Fluids-R.G.Larson
2. Giant Micelles-Properties & Applications-R.Zana & E.W.Kaler

About Malvern Panalytical

Malvern Panalytical provides the materials and biophysical characterization technology and expertise that enable scientists and engineers to understand and control the properties of dispersed systems.

These systems range from proteins and polymers in solution, particle and nanoparticle suspensions and emulsions, through to sprays and aerosols, industrial bulk powders and high concentration slurries.

Used at all stages of research, development and manufacturing, Malvern Panalytical’s materials characterization instruments provide critical information that helps accelerate research and product development, enhance and maintain product quality and optimize process efficiency.

Sponsored Content Policy: News-Medical.net publishes articles and related content that may be derived from sources where we have existing commercial relationships, provided such content adds value to the core editorial ethos of News-Medical.Net which is to educate and inform site visitors interested in medical research, science, medical devices and treatments.