This article assesses the fractional error in Mw that results when θ=90o detection is used instead of a full angular extrapolation via MALS.
Is it possible to contrast the differences in calculating Mw with multi-angle light scattering (MALS) and a single-angle assessment of light scattering?
For polymers and colloids in the nanoscale range, calculating Mw by static light scattering can usually be carried out via multi-angle light scattering (MALS).
Most modern MALS utilizes vertically polarized incident light, with detection occurring in the plane perpendicular to the vertical electric polarization plane, known as the ‘scattering plane.’
If a scatterer’s characteristic dimension is significantly less than the incident wavelength λ, then the particle is called a ‘Rayleigh scatterer,’ with equal scattering intensity across every angle of the scattering plane. In these situations, calculating the scattering intensity at one angle is sufficient to calculate Mw.
An example of where one angle measurement is sufficient is a native monoclonal antibody, measuring (~10 nm)<<λ. When the characteristic dimension is a considerable fraction of λ, it is essential to assess scattering intensity at different angles and extrapolate to zero angle, θ=0, to calculate Mw.
Is it possible to review Raleigh scattering (mentioned above)?
There are numerous layers of approximation to consider when analyzing light scattering information. The Rayleigh approximation is the simplest, as the scattering has no major angular dependence. After this, the Rayleigh-Debye approximation is commonly utilized.
This approximation presumes that scattering's angular dependence occurs from phase differences at the detection angle θ caused solely by the geometrical path length differences between scattering elements in a scattering body.
Since the scatterers resemble threads immersed in a solvent, this is typically a good approximation for polymers. The Rayleigh-Debye range is more limited for solid colloids because the phase shift at the detector between scattering elements is caused by the differences in their geometrical path and the index of refraction contrast that occurs between the solid object and the solvent.
What connection does this have to virial coefficients and the Zimm equation?
The Zimm equation for dilute polymer solutions that results in the Rayleigh-Debye approximation is
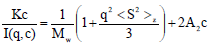 |
Equation 1 |
where I(q,c) is the excess Rayleigh scattering ratio (in units of cm-1), the quantity assessed by the light scattering instrument, identical to its value from the polymer solution subtracting the pure solvent’s value.
In equation 1, q refers to the typical scattering wave-vector amplitude, q=(4πn/λο)sin(θ/2), where n denotes the solvent index of refraction, λο represents the vacuum wavelength of the incident light, dn/dc refers to the differential refractive index for the polymer in the selected solvent, A2 refers to the second virial coefficient (also known as B22), and <S2>z represents the mean square radius of gyration. K is an optical constant for vertically polarized incident light.
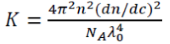 |
Equation 2 |
Considering the term involving A2 is possible if A2’s value has been defined. It may also be ignored if 2A2cMw<<1.
How does this relate to the error while calculating Mw? Moreover, how does this apply to a tool with a single angle at 900, such as ARGEN?
Within this paradigm, it is possible to readily evaluate the mistake in Mw. I(0,c) represents the Rayleigh ratio extrapolated to θ=0, while I(q≠0,c) refers to the observed value at any θ>0. If this last value is utilized, an apparent Mw is calculated and defined as Mw’, smaller than the true Mw. Equation 1 (either accounting for A2 or ignoring it) provides the ratio of Mw’ to Mw as follows:
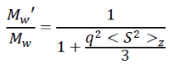 |
Equation 3 |
Adopting values that are suitable for ARGEN applied to aqueous solutions, λ0=660nm, n=1.33, θ=90ο, the equation 3 turns into
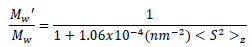 |
Equation 4 |
How are these equations related to product development? For instance, a monoclonal antibody (mAb)?
To begin with, consider the Mw error for a native mAb with a usual hydrodynamic diameter of DH=10 nm. The association between a spheroidal object’s DH and <S2>1/2 is as follows
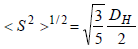 |
Equation 5 |
Substituting <S2>1/2=3.87 nm into equation 5 demonstrates that the error in Mw for a common native mAb is just 0.16 % when utilizing ARGEN.
Figure 1 depicts the fractional underestimate inaccuracy of Mw vs Rg=<S2>1/2 and for equivalent spheroidal DH.
It is crucial to remember that complete angular extrapolation of MALS under the Zimm approximation will also fail when the characteristic dimension of the scatterers nears λ.
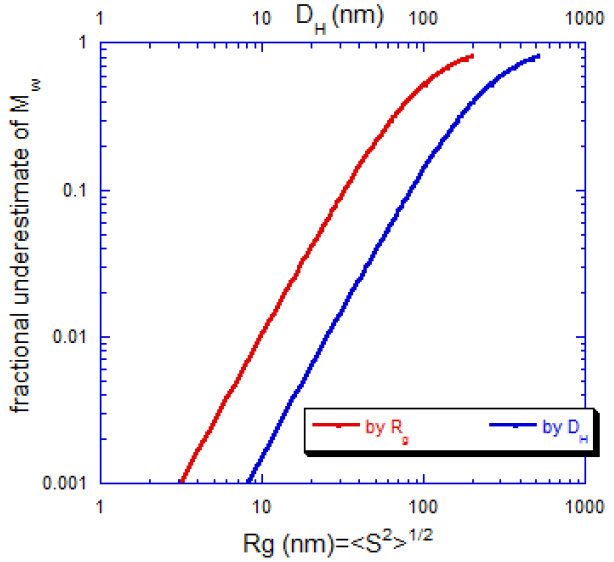
Figure 1. Fractional Mw underestimates at 90° detection. Image Credit: Yokogawa Fluence Analytics
What is the conclusion on the limits of 900 static light scattering for calculating weight average molar mass Mw?
Utilizing ARGEN’s θ=900 detection, globular proteins of the same density (such as mAbs) can be assessed up to 304M0 or 4.16x107g/mol with a 10 % error.
About Yokogawa Fluence Analytics
Yokogawa Fluence Analytics, which was named as a Top 50 global advanced manufacturing startup by CB Insights, provides patented process analytics and control solutions to polymer and biopharmaceutical customers worldwide. Yokogawa Electric Corporation acquired Fluence Analytics in January 2023.
Yokogawa Fluence Analytics is a global leader in real-time polymer reaction monitoring and control, and its industry-leading ACOMP product is the only commercially available smart manufacturing system that continuously monitors and measures polymerization reactions.
The company’s biopharmaceutical product line includes a high-throughput static light scattering instrument called ARGEN. ARGEN can independently measure the stability of biopolymers under thermal, chemical, and mechanical (physical) stress, while also performing shelf-life stability studies at low temperatures.
Sponsored Content Policy: News-Medical.net publishes articles and related content that may be derived from sources where we have existing commercial relationships, provided such content adds value to the core editorial ethos of News-Medical.Net which is to educate and inform site visitors interested in medical research, science, medical devices and treatments.